Estimate the Volume if the Region Is Rotated About the Y Axis Again Use the Midpoint Rule With N 4
6. Applications of Integration
6.3 Volumes of Revolution: Cylindrical Shells
Learning Objectives
- Summate the book of a solid of revolution by using the method of cylindrical shells.
- Compare the different methods for computing a volume of revolution.
In this section, nosotros examine the method of cylindrical shells, the final method for finding the book of a solid of revolution. Nosotros can utilize this method on the same kinds of solids as the disk method or the washer method; however, with the disk and washer methods, we integrate along the coordinate axis parallel to the centrality of revolution. With the method of cylindrical shells, we integrate forth the coordinate axis perpendicular to the axis of revolution. The ability to choose which variable of integration we want to use can be a significant reward with more complicated functions. Also, the specific geometry of the solid sometimes makes the method of using cylindrical shells more appealing than using the washer method. In the last function of this section, we review all the methods for finding volume that we accept studied and lay out some guidelines to help you determine which method to utilise in a given situation.
The Method of Cylindrical Shells
Once again, we are working with a solid of revolution. Every bit before, we define a region ![]() bounded above past the graph of a office
bounded above past the graph of a office ![]() beneath by the
beneath by the ![]() and on the left and right by the lines
and on the left and right by the lines ![]() and
and ![]() respectively, as shown in (Effigy)(a). We so circumduct this region effectually the
respectively, as shown in (Effigy)(a). We so circumduct this region effectually the ![]() -axis, as shown in (Effigy)(b). Notation that this is different from what we have done before. Previously, regions divers in terms of functions of
-axis, as shown in (Effigy)(b). Notation that this is different from what we have done before. Previously, regions divers in terms of functions of ![]() were revolved around the
were revolved around the ![]() or a line parallel to it.
or a line parallel to it.
As we have washed many times before, sectionalisation the interval ![]() using a regular partition,
using a regular partition, ![]() and, for
and, for ![]() choose a point
choose a point ![]() Then, construct a rectangle over the interval
Then, construct a rectangle over the interval ![]() of superlative
of superlative ![]() and width
and width ![]() A representative rectangle is shown in (Figure)(a). When that rectangle is revolved effectually the
A representative rectangle is shown in (Figure)(a). When that rectangle is revolved effectually the ![]() -axis, instead of a disk or a washer, nosotros become a cylindrical vanquish, as shown in the post-obit figure.
-axis, instead of a disk or a washer, nosotros become a cylindrical vanquish, as shown in the post-obit figure.
To calculate the volume of this shell, consider (Figure).

The beat out is a cylinder, then its book is the cross-sectional area multiplied by the height of the cylinder. The cantankerous-sections are annuli (band-shaped regions—essentially, circles with a pigsty in the middle), with outer radius ![]() and inner radius
and inner radius ![]() Thus, the cross-sectional area is
Thus, the cross-sectional area is ![]() The height of the cylinder is
The height of the cylinder is ![]() And so the book of the shell is
And so the book of the shell is
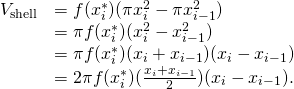
Note that ![]() and so we take
and so we take
![]()
Furthermore, ![]() is both the midpoint of the interval
is both the midpoint of the interval ![]() and the average radius of the crush, and nosotros can approximate this by
and the average radius of the crush, and nosotros can approximate this by ![]() We and so have
We and so have
![]()
Another way to call up of this is to think of making a vertical cut in the shell and then opening it up to grade a flat plate ((Figure)).

In reality, the outer radius of the shell is greater than the inner radius, and hence the dorsum edge of the plate would exist slightly longer than the front border of the plate. Still, we can approximate the flattened trounce by a flat plate of height ![]() width
width ![]() and thickness
and thickness ![]() ((Figure)). The volume of the shell, then, is approximately the volume of the flat plate. Multiplying the meridian, width, and depth of the plate, we get
((Figure)). The volume of the shell, then, is approximately the volume of the flat plate. Multiplying the meridian, width, and depth of the plate, we get
![]()
which is the same formula nosotros had before.
To calculate the volume of the entire solid, nosotros so add the volumes of all the shells and obtain
![]()
Here we have another Riemann sum, this time for the function ![]() Taking the limit as
Taking the limit as ![]() gives u.s.a.
gives u.s.a.
![]()
This leads to the post-obit rule for the method of cylindrical shells.
Now let's consider an example.
The Method of Cylindrical Shells 1
Define ![]() as the region bounded in a higher place by the graph of
as the region bounded in a higher place by the graph of ![]() and below by the
and below by the ![]() over the interval
over the interval ![]() Find the volume of the solid of revolution formed by revolving
Find the volume of the solid of revolution formed by revolving ![]() around the
around the ![]()
Solution
First we must graph the region ![]() and the associated solid of revolution, as shown in the post-obit figure.
and the associated solid of revolution, as shown in the post-obit figure.
Then the volume of the solid is given by
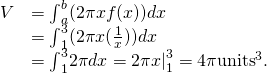
The Method of Cylindrical Shells 2
Define R equally the region bounded to a higher place by the graph of ![]() and below past the
and below past the ![]() over the interval
over the interval ![]() Find the volume of the solid of revolution formed past revolving
Find the volume of the solid of revolution formed past revolving ![]() around the
around the ![]()
Solution
First graph the region ![]() and the associated solid of revolution, as shown in the following figure.
and the associated solid of revolution, as shown in the following figure.
Then the volume of the solid is given by
![Rendered by QuickLaTeX.com \begin{array}{cc}\hfill V& ={\int }_{a}^{b}(2\pi xf(x))dx\hfill \\ & ={\int }_{0}^{2}(2\pi x(2x-{x}^{2}))dx=2\pi {\int }_{0}^{2}(2{x}^{2}-{x}^{3})dx\hfill \\ & ={2\pi \left[\frac{2{x}^{3}}{3}-\frac{{x}^{4}}{4}\right]|}_{0}^{2}=\frac{8\pi }{3}{\text{units}}^{3}\text{.}\hfill \end{array}](https://opentextbc.ca/calculusv1openstax/wp-content/ql-cache/quicklatex.com-b545dcc663fb2d48fc525dc7b018dbac_l3.png)
As with the disk method and the washer method, nosotros can use the method of cylindrical shells with solids of revolution, revolved around the ![]() when we want to integrate with respect to
when we want to integrate with respect to ![]() The analogous rule for this type of solid is given here.
The analogous rule for this type of solid is given here.
The Method of Cylindrical Shells for a Solid Revolved around the 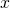 -axis
-axis
For the next case, we await at a solid of revolution for which the graph of a function is revolved around a line other than one of the two coordinate axes. To gear up this up, we demand to revisit the development of the method of cylindrical shells. Retrieve that we institute the volume of one of the shells to be given by
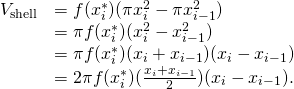
This was based on a shell with an outer radius of ![]() and an inner radius of
and an inner radius of ![]() If, however, we rotate the region around a line other than the
If, however, we rotate the region around a line other than the ![]() we have a unlike outer and inner radius. Suppose, for example, that we rotate the region effectually the line
we have a unlike outer and inner radius. Suppose, for example, that we rotate the region effectually the line ![]() where
where ![]() is some positive abiding. Then, the outer radius of the crush is
is some positive abiding. Then, the outer radius of the crush is ![]() and the inner radius of the shell is
and the inner radius of the shell is ![]() Substituting these terms into the expression for volume, nosotros run across that when a airplane region is rotated around the line
Substituting these terms into the expression for volume, nosotros run across that when a airplane region is rotated around the line ![]() the volume of a vanquish is given by
the volume of a vanquish is given by
![]()
As earlier, we find that ![]() is the midpoint of the interval
is the midpoint of the interval ![]() and can be approximated past
and can be approximated past ![]() And then, the approximate book of the shell is
And then, the approximate book of the shell is
![]()
The remainder of the evolution gain as before, and we see that
![]()
We could too rotate the region around other horizontal or vertical lines, such equally a vertical line in the right half airplane. In each instance, the volume formula must be adjusted accordingly. Specifically, the ![]() in the integral must be replaced with an expression representing the radius of a shell. To encounter how this works, consider the post-obit example.
in the integral must be replaced with an expression representing the radius of a shell. To encounter how this works, consider the post-obit example.
A Region of Revolution Revolved around a Line
For our concluding instance in this section, let's look at the volume of a solid of revolution for which the region of revolution is bounded by the graphs of ii functions.
A Region of Revolution Bounded by the Graphs of Two Functions
Which Method Should Nosotros Utilize?
Nosotros have studied several methods for finding the volume of a solid of revolution, but how do we know which method to utilize? It often comes down to a choice of which integral is easiest to evaluate. (Figure) describes the unlike approaches for solids of revolution around the ![]() Information technology's upwardly to you to develop the analogous table for solids of revolution around the
Information technology's upwardly to you to develop the analogous table for solids of revolution around the ![]()

Permit'south have a look at a couple of additional issues and make up one's mind on the all-time approach to accept for solving them.
Selecting the All-time Method
Solution
- First, sketch the region and the solid of revolution as shown.
Looking at the region, if we want to integrate with respect to
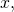 we would accept to interruption the integral into ii pieces, because we accept dissimilar functions bounding the region over
we would accept to interruption the integral into ii pieces, because we accept dissimilar functions bounding the region over ![Rendered by QuickLaTeX.com \left[0,1\right]](https://opentextbc.ca/calculusv1openstax/wp-content/ql-cache/quicklatex.com-871eb0e2e4c0e4f0bfa1d2134a44da2c_l3.png) and
and ![Rendered by QuickLaTeX.com \left[1,2\right].](https://opentextbc.ca/calculusv1openstax/wp-content/ql-cache/quicklatex.com-e5437b7a8c15671d00f848f7fe357a33_l3.png) In this instance, using the disk method, we would have
In this instance, using the disk method, we would have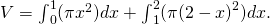
If we used the trounce method instead, we would use functions of
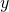 to stand for the curves, producing
to stand for the curves, producing![Rendered by QuickLaTeX.com \begin{array}{cc}\hfill V& ={\int }_{0}^{1}(2\pi y\left[(2-y)-y\right])dy\hfill \\ & ={\int }_{0}^{1}(2\pi y\left[2-2y\right])dy.\hfill \end{array}](https://opentextbc.ca/calculusv1openstax/wp-content/ql-cache/quicklatex.com-3a39b742050ee44cd54513a34ea8526b_l3.png)
Neither of these integrals is particularly onerous, but since the shell method requires only one integral, and the integrand requires less simplification, we should probably become with the shell method in this case.
- Kickoff, sketch the region and the solid of revolution as shown.
Looking at the region, it would be problematic to define a horizontal rectangle; the region is bounded on the left and right by the same role. Therefore, we can dismiss the method of shells. The solid has no cavity in the center, and then we tin use the method of disks. Then
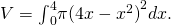
Select the all-time method to find the volume of a solid of revolution generated by revolving the given region effectually the ![]() and gear up upwards the integral to find the volume (do not evaluate the integral): the region bounded by the graphs of
and gear up upwards the integral to find the volume (do not evaluate the integral): the region bounded by the graphs of ![]() and
and ![]()
Solution
Utilize the method of washers; ![]()
Key Concepts
- The method of cylindrical shells is another method for using a definite integral to calculate the volume of a solid of revolution. This method is sometimes preferable to either the method of disks or the method of washers considering we integrate with respect to the other variable. In some cases, one integral is substantially more complicated than the other.
- The geometry of the functions and the difficulty of the integration are the chief factors in deciding which integration method to use.
Key Equations
- Method of Cylindrical Shells
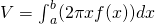
For the following exercise, find the book generated when the region between the ii curves is rotated effectually the given centrality. Utilise both the shell method and the washer method. Utilize engineering science to graph the functions and depict a typical slice by hand.
2. [T] Under the curve of ![]() rotated around the
rotated around the ![]()
Solution

![]() unitsiii
unitsiii
3. [T] Over the bend of ![]() rotated around the
rotated around the ![]()
iv. [T] Under the curve of ![]() rotated around the
rotated around the ![]()
Solution

![]() units3
units3
5. [T] Under the curve of ![]() rotated around the
rotated around the ![]()
6. [T] Under the bend of ![]() rotated around the
rotated around the ![]()
Solution

![]() units3
units3
For the post-obit exercises, use shells to find the volumes of the given solids. Notation that the rotated regions lie between the curve and the ![]() and are rotated around the
and are rotated around the ![]()
7. ![]()
8. ![]()
Solution
![]() unitsthree
unitsthree
9. ![]()
10. ![]()
Solution
![]() unitsthree
unitsthree
11. ![]()
12. ![]()
Solution
![]() units3
units3
thirteen. ![]()
14. ![]()
Solution
![]() unitsiii
unitsiii
xv. ![]()
16. ![]()
Solution
![]() unitsthree
unitsthree
For the following exercises, use shells to find the volume generated by rotating the regions between the given curve and ![]() around the
around the ![]()
17. ![]()
eighteen. ![]()
Solution
![]() units3
units3
19. ![]()
xx. ![]()
Solution
![]() units3
units3
21. ![]()
22. ![]()
Solution
![]() unitsthree
unitsthree
23. ![]()
24. ![]()
Solution
![]() units3
units3
25. ![]()
26. ![]()
Solution
![]() units3
units3
For the post-obit exercises, observe the book generated when the region betwixt the curves is rotated around the given axis.
27. ![]() rotated effectually the
rotated effectually the ![]()
28. ![]() rotated effectually the
rotated effectually the ![]()
Solution
![]() units3
units3
29. ![]() rotated around the
rotated around the ![]()
30. ![]() rotated around the line
rotated around the line ![]()
Solution
![]() unitsiii
unitsiii
31. ![]() rotated around the line
rotated around the line ![]()
32. ![]() rotated effectually the
rotated effectually the ![]()
Solution
![]() unitsiii
unitsiii
33. ![]() rotated around the line
rotated around the line ![]()
34. ![]() rotated effectually the
rotated effectually the ![]()
Solution
![]() units3
units3
35. ![]() rotated around the line
rotated around the line ![]()
For the following exercises, utilise technology to graph the region. Decide which method you remember would exist easiest to utilize to summate the volume generated when the function is rotated around the specified axis. Then, use your called method to find the volume.
38. [T] ![]() rotated around the
rotated around the ![]()
Solution

![]() unitsiii
unitsiii
39. [T] ![]() rotated effectually the
rotated effectually the ![]()
forty. [T] ![]() rotated around the
rotated around the ![]()
Solution

![]() units3
units3
41. [T] ![]() rotated around the
rotated around the ![]()
42. [T] ![]() rotated effectually the
rotated effectually the ![]()
Solution

![]() units3
units3
44. [T] ![]() rotated around the
rotated around the ![]()
Solution

15.9074 units3
For the following exercises, use the method of shells to guess the volumes of some common objects, which are pictured in accompanying figures.
45. Use the method of shells to find the volume of a sphere of radius ![]()

46.Utilise the method of shells to find the volume of a cone with radius ![]() and acme
and acme ![]()

Solution
![]() unitsthree
unitsthree
47.Use the method of shells to find the book of an ellipse ![]() rotated around the
rotated around the ![]()

48.Use the method of shells to notice the volume of a cylinder with radius ![]() and acme
and acme ![]()

Solution
![]() units3
units3
49.Utilise the method of shells to find the volume of the donut created when the circle ![]() is rotated around the line
is rotated around the line ![]()

Glossary
- method of cylindrical shells
- a method of computing the book of a solid of revolution by dividing the solid into nested cylindrical shells; this method is different from the methods of disks or washers in that we integrate with respect to the contrary variable
Source: https://opentextbc.ca/calculusv1openstax/chapter/volumes-of-revolution-cylindrical-shells/
Enregistrer un commentaire for "Estimate the Volume if the Region Is Rotated About the Y Axis Again Use the Midpoint Rule With N 4"